-
日期: 2025-07-07 | 来源: 新智元 | 有0人参与评论 | 字体: 小 中 大
张瑞祥现任加州大学伯克利分校数学系助理教授,2017年获普林斯顿大学数学博士学位,2012年毕业于北京大学数学系
她的想法确实没错——就这样,Cairo解决了所谓的Mizohata?Takeuchi猜想(Mizohata?Takeuchi conjecture)。
该猜想最早在1980年代提出,调和分析 (harmonic analysis) 界研究了几十年。
学界普遍相信它是正确的——因为若它成立,就能自动推导出该领域中多个重要结果。
这下,全场震惊。年仅17岁、还没高中毕业的她,竟然解决了困扰数学界数十年的难题!
在张教授的指导下,她将于今年秋季进入马里兰大学,直接攻读博士学位。
她出生在巴哈马首都拿骚(Nassau),后来搬到美国,就读高中,但也在加州大学伯克利分校 (UC Berkeley) 上过课。
她回忆道:「我给几位教授写邮件,介绍自己读过哪些相关书,并询问能否旁听。他们很多人都同意,包括张教授。」
有一天,张教授出了一个练习题:证明Mizohata?Takeuchi猜想某个特殊但更简单的情形。作为选做题,他还给出了原始猜想。
自那时起,Cairo就完全被它吸引住了。
40年难未解之谜Mizohata?Takeuchi猜想Mizohata?Takeuchi猜想属于调和分析领域,而调和分析的目的是将函数分解成更简单的成分,比如正弦函数。
陶哲轩介绍过:「调和分析作为分析学的重要分支,其核心关注点在于对函数性质的定量刻画。与传统定性研究不同,该领域致力于建立精确的数值界。」
如今,调和分析研究非常活跃,并已成为从数字音视频压缩到电信系统设计等诸多应用中的基础工具。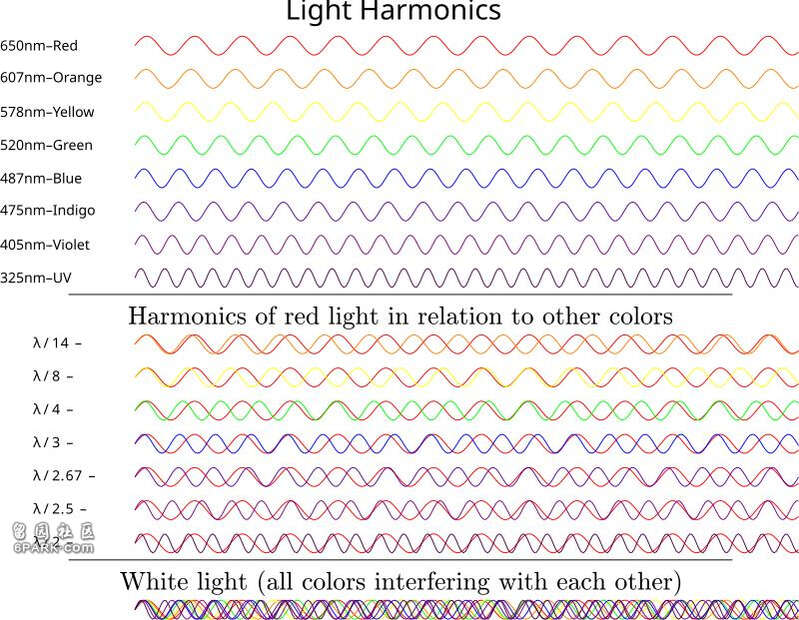
- 新闻来源于其它媒体,内容不代表本站立场!
-
原文链接
原文链接:
目前还没有人发表评论, 大家都在期待您的高见