-
日期: 2016-05-07 | 來源: 張偉偉博客 | 有0人參與評論 | 專欄: 美東颶風 | 字體: 小 中 大
去過游樂場的同學應該對“颶風飛椅”不陌生,壹張大傘下利用軟繩拉著許多椅子。當大傘靜止不動時,軟繩垂直向下,當大傘旋轉以後,在軟繩的拉力作用下人坐的椅子會向外展開“飛”了起來。在旋轉的過程中“傘面”會發生傾斜,增加游樂的趣味性。那麼這個“飛椅”是靠什麼原理“飛”起來的呢?

太原迎澤公園

和向心力相對應的另外壹個概念是離心力,它的方向背離圓周運動中心。我們可以這樣理解,由於離心力和向心力的平衡,做圓周運動的物體才沒有靠近運動中心也沒有遠離運動中心。不過需要強調的是,離心力是壹個慣性力,離心力只存在於做圓周運動(或曲線運動)中,就像坐汽車在快速轉彎的時候有壹種要被“甩”出去的感覺,那就是離心力的作用。
有了這兩個概念,我們來看飛椅是如何飛起來的。當飛椅從靜止開始旋轉後,由於物體有保持其原始“運動狀態”的慣性,就形成了離心力,椅子有遠離運動中心的趨勢,但由於拉繩作用,結果就是拉繩向外偏離壹個角度,這個角度的產生,使得繩子的拉力和重力可以合成指向運動中心的力——向心力(如下圖中紅色標注的力),當向心力和離心力平衡後,使得人椅可以維持圓周運動。

為了簡化分析,我們考慮只有兩把椅子的情況,如上圖所示。並且將椅子作為質點考慮。初始情況,繩子下垂,即θ=0,說椅子飛起來了,實際上就是θ不等於0的情況。假設旋轉後,BC處於水平狀態,設|OC|=a,繩子的長度為l,則椅子的實際旋轉半徑為r=a+lsinθ,因此繩子的張力和向心力的公式為:

向心力是物體做圓周運動的必要條件,當軟繩初始垂直於傘面時,即θ=0,就有sinθ=0,根據公式(2),就不能產生向心力,椅子也就不能維持圓周運動。只有θ不為0才能產生向心力,壹旦θ不為0,我們就看到椅子“飛”起來了。
如果有人想特別刺激壹點,讓旋轉速度特別大,椅子飛的特別高,那麼飛椅有可能飛的超過“傘面”高度嗎?不可能,上面的問題用力學的術語講就是討論θ角有沒有可能超過90度?從(1)式可以看出,繩子的張力為:FT=mg/cosθ,這意味著如果θ趨近於90度,拉繩的張力將會趨於無窮大,由於繩子所能承受的最大拉力是有限的,所以,椅子不能“飛”到與“傘面”等高的高度,也不能再向高處飛去。
既然不可能超過傘面,那拉繩偏離角度θ最大值由什麼確定?如果我們不考慮電機功率的影響因素,可提供任意的轉速。拉繩的最大偏離角可由(1)式決定。假定在實驗中可以測定繩子的最大拉力為Fc,那麼拉繩的最大偏離角θ可由下式決定cosθ=mg/Fc,注意,這裡的Fc是通過實驗測定的表征繩子抗拉能力的常數。通常情況下,為了安全,會設定壹個安全系數n,例如n=4,則cosθ= 4mg/Fc。
還有壹個問題我們比較感興趣,將式(1)和(2)做比,可得到公式(3)
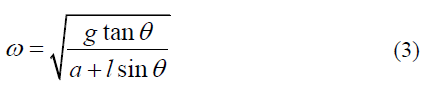
這說明拉繩的偏離角度θ和轉速有對應關系,為了直觀了解θ與w之間的關系,我們假設繩長度為l=3.5m,懸掛點離開圓心的距離a=1.5m,繪制θ與w之間的關系曲線,如下

橫坐標為角速度,縱坐標為拉繩偏離角度
從上圖可以粗略看出,旋轉速度在1rad/s到2rad/s時變化時,拉繩的偏離角度變化率最大。旋轉速度有微小變化時,飛椅的飛行高度就會有比較明顯的變化,轉動在這個區間內,人的體驗可能更加刺激。- 新聞來源於其它媒體,內容不代表本站立場!
-
原文鏈接
原文鏈接:
目前還沒有人發表評論, 大家都在期待您的高見