-
日期: 2025-10-28 | 来源: 煎蛋网 | 有0人参与评论 | 字体: 小 中 大
从王子打赌到现代算法,数学家终于发现一种特殊多面体——Noperthedron,它无法通过任何方式让自身穿过自身,打破了几何学中延续三百年的猜想。
想象你手中有两颗大小相同的骰子。如果在其中一颗上钻一条直通的隧道,另一颗能顺利穿过吗?
“当然不可能吧?”大多数人都会这样想。十七世纪末,一位身份不明的人和莱茵的Nopert王子打了这样一个赌。Nopert是英王查理一世的侄子,曾指挥保皇党军队,晚年在温莎城堡里研究金属和玻璃。
他赢了赌局。数学家John Wallis在1693年记载了这件事——没人知道Nopert是写了证明,还是真的在方块上钻了洞。但Wallis自己证明了:如果沿立方体内部的一条对角线方向钻洞,孔径确实可以让另一颗相同的立方体穿过。只要第二颗方块大4%,就再也过不去了。
自那以后,人们开始好奇,还有哪些形状也能“穿过自己”。Google工程师Tom Murphy说,这个问题“太经典了,连外星人都会重新发现它。”
数学家通常研究的是凸多面体——像立方体那样表面平整、没有凹陷的几何体。如果某个形状在某些方向上更宽,就容易找到一条直线通道,让另一个相同的形状穿过。但许多著名的多面体,如十二面体或截角二十面体(足球的形状),对称性太高,难以分析。
“几百年来,我们只知道立方体具备这种特性,”奥地利统计局的数学家Jakob Steininger说。
直到1968年,数学家Christoph Scriba证明了四面体和八面体也拥有这种“Nopert性质”。此后十年,数学家和几何爱好者不断发现更多例子,包括十二面体、二十面体和足球体。Nopert性质似乎无处不在,甚至有人大胆猜测:所有凸多面体都能穿过自身。
没人能反驳——直到今年。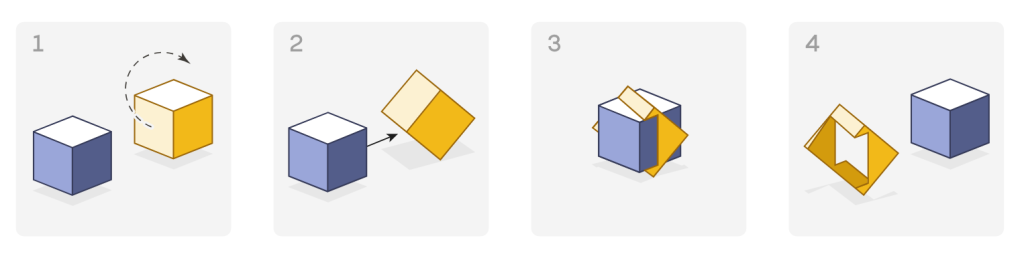
把一个立方体的角倒过来,另一个立方体就可以通过。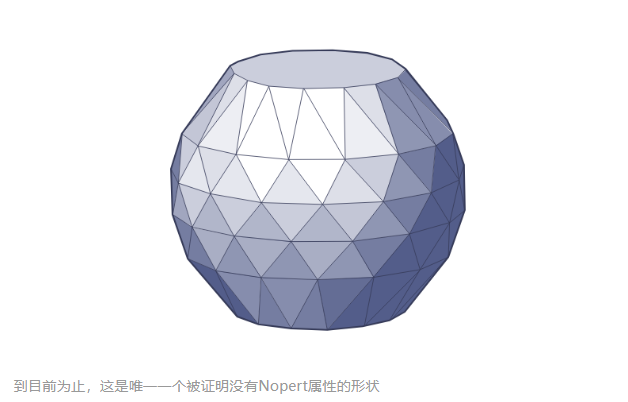
2025年8月,Steininger与奥地利研究员Sergey Yurkevich发表论文,描述了一种拥有90个顶点、152个面的新形状——他们命名为“Noperthedron”,名字由Murphy创造,意为“Nopert(Rupert)”的反面——“不行(nope)”。他们证明,无论怎样钻直线隧道,第二个Noperthedron都无法通过。
证明过程既依赖理论突破,也依靠庞大的计算。这个形状的顶点分布极其微妙,Steininger感叹:“能成功简直是奇迹。”
要理解立方体如何穿过自己,可以想象一只立方体的“影子”。如果立方体放平,影子是正方形;若将一个角朝上,影子则变成正六边形。Wallis发现,正方形影子刚好能嵌入六边形中,于是沿垂直方向钻洞,另一颗立方体就能穿过。一个世纪后,Pieter Nieuwland找到更好的角度,使通道能容纳比原立方体大6%的方块。- 新闻来源于其它媒体,内容不代表本站立场!
-
原文链接
原文链接:
目前还没有人发表评论, 大家都在期待您的高见